Circles पर संशोधन नोट्स
वृत्त
एक निश्चित बिंदु से समान दूरी पर स्थित सभी बिंदुओं से बनी आकृति को वृत्त कहते हैं।
1. केंद्र
निश्चित बिंदु को वृत्त के केंद्र के रूप में जाना जाता है।
2. त्रिज्या
वृत्त के किसी भी बिंदु से निश्चित बिंदु तक की दूरी त्रिज्या है। केंद्र और वृत्त के किसी बिंदु को मिलाने वाला कोई भी रेखाखंड त्रिज्या कहलाता है।
3. राग
वृत्त की सीमा पर किन्हीं दो बिन्दुओं को मिलाकर बना कोई भी रेखाखण्ड जीवा कहलाता है।
4. व्यास
व्यास त्रिज्या का दो गुना है। यह वृत्त की सबसे लंबी जीवा है जो केंद्र से होकर गुजरती है। सभी व्यासों की लंबाई समान होती है।
5. परिधि
वृत्त की सीमा की लंबाई वृत्त की परिधि कहलाती है।
6. चाप
एक चाप वृत्त की परिधि पर दो बिंदुओं को मिलाने वाले वृत्त का हिस्सा है।
7. सेक्टर
एक चाप और वृत्त की दो त्रिज्याओं द्वारा केंद्र को चाप के अंतिम बिंदुओं से जोड़कर बनाया गया क्षेत्र त्रिज्यखंड कहलाता है।
8. खंड
वृत्त की एक जीवा और एक चाप द्वारा बनाया गया क्षेत्र खंड कहलाता है।
एक समतल में एक वृत्त और एक रेखा के बीच संबंध
एक रेखा और एक वृत्त होने पर तीन स्थितियाँ हो सकती हैं।
1. गैर-प्रतिच्छेदी रेखा
जब एक रेखा और एक वृत्त का कोई उभयनिष्ठ बिंदु नहीं होता है तो इसे वृत्त के संबंध में एक अप्रतिच्छेदी रेखा कहा जाता है।
2. छेदक
जब कोई रेखा किसी वृत्त को इस प्रकार काटती है कि दो उभयनिष्ठ बिंदु होते हैं तो वह रेखा छेदक रेखा कहलाती है।
3. स्पर्शरेखा
जब कोई रेखा वृत्त को इस प्रकार स्पर्श करती है कि उनमें केवल एक उभयनिष्ठ बिंदु होता है तो उस रेखा को स्पर्श रेखा कहते हैं। उस सामान्य बिंदु को संपर्क बिंदु कहा जाता है।
एक वृत्त की स्पर्शरेखा
किसी वृत्त की सभी स्पर्श रेखाएँ उस स्पर्श रेखा के स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लम्बवत् होती हैं।
OP वृत्त की त्रिज्या है और Q रेखा XY पर कोई बिंदु है जो वृत्त की स्पर्श रेखा है। चूंकि OP बिंदु O से XY के बिंदुओं तक की सभी दूरियों की सबसे छोटी रेखा है। अतः OP, XY के लंबवत है। इसलिए, OP⊥ XY
उदाहरण
दी गई आकृति में वृत्त की त्रिज्या ज्ञात कीजिए, यदि बिंदु A से स्पर्श रेखा की लंबाई, जो केंद्र से 5 सेमी दूर है, 4 सेमी है।
समाधान
जैसा कि हम जानते हैं कि त्रिज्या, त्रिज्या के लंबवत होती है, इसलिए ∆ABO एक समकोण त्रिभुज है।
दिया गया है, AO = 5 सेमी और AB = 4 सेमी
हम यहाँ पाइथागोरस प्रमेय का उपयोग कर सकते हैं
ओए 2 = ओबी 2 + एबी 2
ओबी 2 = ओए 2 - एबी 2
= 5 2 - 4 2
= 25 - 16
ओबी 2 = 9
ओबी = 3
अतः दिए गए वृत्त की त्रिज्या 3 सेमी है
एक वृत्त पर एक बिंदु से स्पर्शरेखाओं की संख्या
1. स्पर्श के एक बिंदु पर केवल एक ही स्पर्श रेखा हो सकती है।
2. वृत्त के भीतर किसी बिंदु से स्पर्श रेखा नहीं खींची जा सकती।
3. वृत्त के बाहर किसी बिंदु से वृत्त पर केवल दो स्पर्श रेखाएँ हो सकती हैं।
किसी बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती हैं।
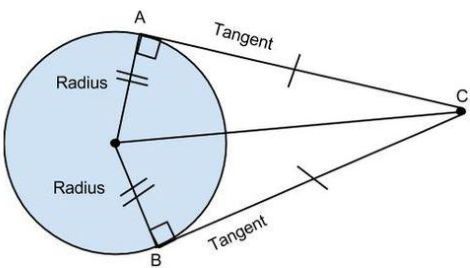
यहाँ, बाह्य बिंदु C से दो स्पर्श रेखाएँ खींची गई हैं। चूँकि स्पर्श रेखा त्रिज्या के लंबवत है, इसने समकोण त्रिभुज का निर्माण किया।
अतः ∆AOC और ∆BOC सर्वांगसम समकोण त्रिभुज हैं। इसलिए एसी = बीसी।
उदाहरण
यदि O केंद्र वाले बिंदु P से वृत्त पर दो स्पर्श रेखाएँ PA और PB खींची जाएँ और OP वृत्त के व्यास के बराबर हो तो दर्शाइए कि त्रिभुज APB एक समबाहु त्रिभुज है।
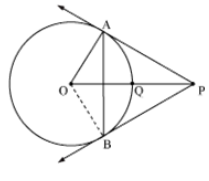
समाधान
दिया गया है, AP वृत्त की स्पर्श रेखा है।
इसलिए, OA ⊥ AP (स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब है)
∠OAP = 90°
∆OAP में,
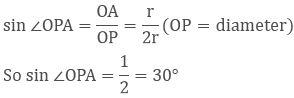
इसी प्रकार, हम सिद्ध कर सकते हैं कि ∠OPB = 30° है
अब, ∠APB = ∠OPA + ∠OPB = 30° + 30° = 60°
∆PAB में, PA = PB (बाह्य बिंदु से स्पर्श रेखाओं की लंबाई बराबर होती है)
∠PAB = ∠PBA (समान भुजाओं के सम्मुख कोण बराबर होते हैं)
∠PAB + ∠PBA + ∠APB = 180° (कोण योग गुण के कारण)
∠PAB + ∠PBA = 180° - 60°
2∠PAB = 120
∠PAB = 60°
क्योंकि ∠PAB = ∠PBA = ∠APB = 60° है
अतः PAB एक समबाहु त्रिभुज है।
उदाहरण
दिए गए वृत्त में AB की लंबाई ज्ञात कीजिए, जो बाहरी वृत्त में जीवा है और आंतरिक वृत्त की स्पर्श रेखा है। आंतरिक और बाहरी वृत्त की त्रिज्या क्रमशः 6 सेमी और 10 सेमी है।
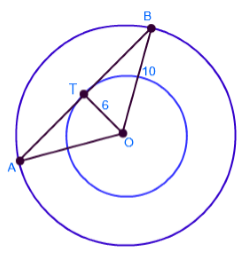
समाधान
दिया गया
भीतरी वृत्त की त्रिज्या (r) = 6 सेमी
बाहरी वृत्त की त्रिज्या (R) = 10 सेमी
बिंदु T के रूप में जो स्पर्शरेखा बिंदु है, जीवा का मध्य बिंदु है, AT = TB
चूंकि त्रिज्या स्पर्शरेखा के लंबवत है,
तो एक समकोण त्रिभुज है और हम पाइथागोरस प्रमेय का उपयोग कर सकते हैं।
ओबी 2 = ओटी 2 + टीबी 2
टीबी 2 = ओबी 2 - ओटी 2
= 10 2 - 6 2
= 100 - 36
टीबी 2 = 64
टीबी = 8 सेमी
एबी = टीबी + एटी
एबी = 8 + 8 (एटी = बीटी)
एबी = 16 सेमी
0 Comments